Determinar el valor final de una renta pospagable, mensual, de 10 años de duración, que experimenta incrementos acumulados cada año del 4,0%, y que dentro de cada año es constante. La primera mensualidad es de 500 €. La mensualidad número 4 de cada año no se entrega. Valorar al 6,0% efectivo anual.
Vea en el blog la resolución de un caso similar.
La fórmula de la celda F13 es la siguiente:
=PERSONAL.XLSB!VFgeo(VF(C14;12;-C12)-C12*(1+C14)^(12-C17);C16;C11;C13)
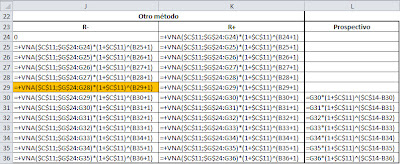
Veamos tres métodos de resolución.
Las faltas.