Hasta ahora hemos visto los préstamos simples. Un préstamo simple es aquel que está compuesto únicamente por un capital perteneciente a la prestación (Co;0) y un capital perteneciente a la contraprestación (Cn;n), no existiendo más pagos.
En este tipo de préstamos aunque se denominen préstamos simples se aplica la ley de la capitalización compuesta.
Cn=Co(1+i)^n
Ahora nos centraremos en los préstamos de prestación única y contraprestación múltiple. En estos préstamos se ha de cumplir que la prestación ha de ser igual a la contraprestación valoradas ambas en el mismo instante del tiempo, sea cual sea este.
Ejemplo
Supongamos un préstamo cuya prestación es el principal de importe 100.000 € que entrega el prestamista al prestatario. Supongamos que el prestamista es el banco y el prestatario es su cliente. El prestatario devolverá este importe prestado junto con sus intereses mediante la entrega de cuatro términos anuales de importes:- 35.000 € en t=1
- 32.500 € en t=2
- 30.000 € en t=3
- 27.500 € en t=4
El préstamo se ha pactado al 10% anual.
Realizando la Equivalencia Financiera en t=0 igualamos los 100.000 € de la prestación, que ya están en t=0 con el valor actual de la renta que se ha de pagar descontando al 10% anual.
Veamos el esquema dinámico. Este es un caso en el que todos los años amortizamos la misma cantidad. Como son 4 años y tenemos que amortizar 100.000 € cada año tenemos que amortizar 25.000 €. Esta cifra se obtienen dividiendo 100.000 entre 4.
Siempre se cumple que el término amortizativo es igual a la cuota de intereses más la cuota de amortización.
La cuota de intereses se obtiene multiplicando el tipo de interés (i) por el capital vivo del periodo anterior.
Veamos el esquema dinámico. Este es un caso en el que todos los años amortizamos la misma cantidad. Como son 4 años y tenemos que amortizar 100.000 € cada año tenemos que amortizar 25.000 €. Esta cifra se obtienen dividiendo 100.000 entre 4.
Siempre se cumple que el término amortizativo es igual a la cuota de intereses más la cuota de amortización.
La cuota de intereses se obtiene multiplicando el tipo de interés (i) por el capital vivo del periodo anterior.

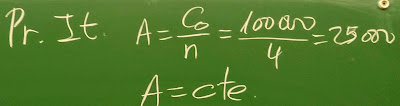




Adolfo, no entiendo la relación entre la operación que hacemos en la primera foto y el gráfico posterior. ¿Cómo resolveríamos el ejercicio?
ResponderEliminarHola Bel.
EliminarLa primera imagen de pizarra nos muestra el denominado "esquema estático" de la operación, donde se anotan las cuantías que intervienen a lo largo de una recta que representa la renta. Se indica la prestación que es Co=100.000 € y vence en t=0. También se indica la contraprestación que está formada por cuatro cuantías a1, a2, a3 y a4 que vencen en los instantes 1, 2, 3 y 4 respectivamente.
En esta primera imagen también se hace la Equivalencia Financiera en t=0. Esto supone igualar Prestación y Contraprestación ambas valoradas en t=0. Sale una ecuación valorando a un tanto anual del 10% donde no hay ninguna incógnita pero se puede comprobar que el resultado es 100.000.
El segundo gráfico es el denominado "esquema dinámico" de la operación financiera donde se representa en altura la evolución del saldo de la operación. Puedes observar que se parte de Co=100.000 €, luego crece el saldo por efecto del paso del tiempo durante le primer año y por efecto de los intereses tabajando al 10%. Se llega hasta 110.000 € en t=1 (Reserva en 1 por la izquierda). En ese mismo instante se paga el primer término amortizativo a1 de importe 35.000 € (esto es un dato del problema). Puesto que el término amortizativo tiene dos componentes donde parte son intereses y parte es amortización se cumple que a1=I1+A1. La cuota de intereses I1 es igual a 10.000 € ya que es el 10% de 100.000, por tanto A1 es igual a la diferencia A1=35.000-10.000=25.000 €.
El capital vivo en t=1 es C1 que es la reserva matemática en 1 por la derecha. Se puede ver en el gráfico que es igual a 75.000 €. Esta cifra se obtienen restando los 100.000 € que son los que inicialmente debíamos al banco menos los 25.000 € que hemos amortizado.
Durante el resto de los años se sigue el mismo procedimiento.
De esta forma en el "esquema dinámico" se puede ver que el capital vivo o deuda pendiente al final de cada periodo va disminuyendo hasta que al final se hace cero.
Un saludo.